Engineering to enhance human mobility, play, and exploration
Congratulations to Dr. Charlotte DeVol Caskey on earning her Doctorate in Mechanical Engineering! Dr. Caskey’s PhD thesis dissertation was titled Effects of Spinal Stimulation on Neuromechanics of Gait for Children with Cerebral Palsy. Congratulations and best of luck as you move forward as a Postdoc in the Human Neuromechanics Laboratory at the University of Florida in Gainesville!
On May 14, 2024, Steele Lab members Dr. Megan Ebers, Mackenzie Pitts, and Dr. Kat Steele attended the Women in Data Science (WiDS) Puget Sound conference hosted at Seattle University. WiDS aims to inspire and educate data scientists worldwide, regardless of gender, and to support women in the field.
Among the speakers at the conference, postdoctoral scholar Dr. Megan Ebers gave a presentation titled “Data Expansion to Improve Accuracy and Availability of Digital Biomarkers for Human Health and Performance.”
Journal Article in Scientific Reports
Ankle exoskeletons alter whole-body walking mechanics, energetics, and stability by altering center-of-mass (CoM) motion. Controlling the dynamics governing CoM motion is, therefore, critical for maintaining efficient and stable gait. However, how CoM dynamics change with ankle exoskeletons is unknown, and how to optimally model individual-specific CoM dynamics, especially in individuals with neurological injuries, remains a challenge.
Aim: Evaluate individual-specific changes in CoM dynamics in unimpaired adults and one individual with post-stroke hemiparesis while walking in shoes-only and with zero-stiffness and high-stiffness passive ankle exoskeletons.
Methods: To identify optimal sets of physically interpretable mechanisms describing CoM dynamics, termed template signatures, we leveraged hybrid sparse identification of nonlinear dynamics (Hybrid-SINDy), an equation-free data-driven method for inferring sparse hybrid dynamics from a library of candidate functional forms.
Results: In unimpaired adults, Hybrid-SINDy automatically identified spring-loaded inverted pendulum-like template signatures, which did not change with exoskeletons (p > 0.16), except for small changes in leg resting length (p < 0.001). Conversely, post-stroke paretic-leg rotary stiffness mechanisms increased by 37–50% with zero-stiffness exoskeletons.
Interpretation: While unimpaired CoM dynamics appear robust to passive ankle exoskeletons, how neurological injuries alter exoskeleton impacts on CoM dynamics merits further investigation. Our findings support Hybrid-SINDy’s potential to discover mechanisms describing individual-specific CoM dynamics with assistive devices.
Steele lab member and postdoctoral scholar, Megan Ebers, was featured in the Winter 2024 UW Data Science Seminar series. You can watch her full presentation on “Mobile sensing with shallow recurrent decoder networks” linked HERE on UW eScience Institute’s YouTube channel.
Abstract: Sensing is a fundamental task for the monitoring, forecasting, and control of complex systems. In many applications, a limited number of sensors are available and must move with the dynamics, such as with wearable technology or ocean monitoring buoys. In these dynamic systems, the sensors’ time history encodes a significant amount of information that can be extracted for critical tasks. We show that by leveraging the time-history of a sparse set of sensors, we can encode global information of the measured high-dimensional system using shallow recurrent decoder networks. This paradigm has important applications for technical challenges in climate modeling, natural disaster evaluation, and personalized health monitoring; we focus especially on how this paradigm has the potential to transform the way we monitor and manage movement-related health outcomes.
Bio: Megan Ebers is a postdoctoral scholar in applied mathematics with UW’s NSF AI Institute in Dynamic Systems. In her PhD research, she developed and applied machine learning methods for dynamics systems to understand and enable human mobility. Her postdoctoral research focuses on data-driven and reduced-order methods for complex systems, so as to continue her work in human-centered research challenges, as well as to extend her research to a broader set of technical challenges, including turbulent flow modeling, natural disaster monitoring, and acoustic object detection.
Journal Article in SIAM Journal on Applied Dynamical Systems
Physics-based and first-principles models pervade the engineering and physical sciences, allowing for the ability to model the dynamics of complex systems with a prescribed accuracy. The approximations used in deriving governing equations often result in discrepancies between the model and sensor-based measurements of the system, revealing the approximate nature of the equations and/or the signal-to-noise ratio of the sensor itself. In modern dynamical systems, such discrepancies between model and measurement can lead to poor quantification, often undermining the ability to produce accurate and precise control algorithms.
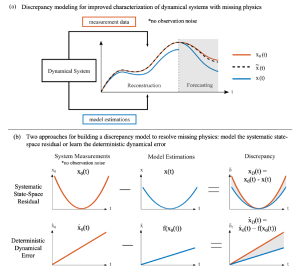
Aim: Introduce a discrepancy modeling framework to identify the missing physics and resolve the model-measurement mismatch with two distinct approaches: (i) by learning a model for the evolution of systematic state-space residual, and (ii) by discovering a model for the deterministic dynamical error. Regardless of approach, a common suite of data-driven model discovery methods can be used.
Method: Specifically, we use four fundamentally different methods to demonstrate the mathematical implementations of discrepancy modeling: (i) the sparse identification of nonlinear dynamics (SINDy), (ii) dynamic mode decomposition (DMD), (iii) Gaussian process regression (GPR), and (iv) neural networks (NN). The choice of method depends on one’s intent (e.g., mechanistic interpretability) for discrepancy modeling, sensor measurement characteristics (e.g., quantity, quality, resolution), and constraints imposed by practical applications (e.g., state- or dynamical-space operability).
Results: We demonstrate the utility and suitability for both discrepancy modeling approaches using the suite of data-driven modeling methods on three continuous dynamical systems under varying signal-to-noise ratios. Finally, we emphasize structural shortcomings of each discrepancy modeling approach depending on error type.
Interpretation: In summary, if the true dynamics are unknown (i.e., an imperfect model), one should learn a discrepancy model of the missing physics in the dynamical space. Yet, if the true dynamics are known yet model-measurement mismatch still exists, one should learn a discrepancy model in the state space.